Sorting Algorithms הוא שם כללי לקבוצת אלגוריתמים אשר מטרתם לסדר מערך. במאמר זה נעבור על מספר אלגוריתמים שימושיים ונסביר את עקרון פעולתם.
בשפת – #C קיימות פונקציות מובנות לסידור מערכים, ()Array.Sort למשל.
כאשר אנו קוראים לפונקציה זו, היא מחזירה לנו את המערך ששלחנו לה בסדר עולה.
פעולה שנשמעת תמימה למדי, אך למעשה, אם היה ברשותנו מערך גדול,
והיה עלינו לסדר אותו ללא שימוש בפונקציה הייעודית של #C,
כנראה שהיינו בונים אלגוריתם בעצמנו, ויש מספר דרכים לעשות זאת.
חלק מהפתרונות היו מובילים לכך שמספר הריצות שהיה נדרש על מנת לבצע את הסידור עלול היה להיות גדול מדי,
במאמר זה נעבור על חלק מהאלגוריתמים הנפוצים בשימוש ונבדוק מי היעיל מבינם.
החלפת אלמנטים במערך
נתחיל עם פונקציה פשוטה שמטרתה להחליף מיקומים במערך:
public static void Exchange(int[] data, int index1, int index2)
{
int temp;
temp = data[index1];
data[index1] = data[index2];
data[index2] = temp;
}
בפונקציה זו נשתמש במהלך הדוגמאות של מאמר זה,
כלומר שבכל פעם שנרצה לשנות סדר במערך נוכל להשתמש בה.
אם נרצה, נוכל למשל לממש אותה כך:
int[] vs = { 13456, 23476, 3365765, 43567, 5356, 635675, 756 };
Exchange(vs, 0, 3);
vs.ToList().ForEach(x => Console.WriteLine(x));
כלומר שבדוגמא זו האלמנט הראשון יחליף את מקומו עם האלמנט הרביעי.
Bubble Sort
זהו אלגוריתם אשר עקרון הפעולה שלו הוא כזה שהוא "סורק" כל פעם את הרשימה,
אם נמצא אלמנט באינדקס שגוי אז מטפל בו.
אנו מגדירים לו כל פעם את מספר ההחלפות כמספר האלמנטים הלא מסודרים שנשארו,
כלומר שלאחר כל החלפה\ריצה של הלולאה יתעדכן נתון זה.
שימו לב ל-Code Snippet הבא:
public static string BubbleSort(int[] data)
{
int num1 = 0, num2 = 0, num3 = 0;
for (int j = data.Length - 1; j > 0; j--)
{
num1++;
for (int i = 0; i < j; i++)
{
num2++;
if (data[i] > data[i + 1])
{
num3++;
Exchange(data, i, i + 1);
}
}
}
return $"outer ring: {num1}\ninner ring:{num2}\nexchanges: {num3}";
}
את המשתנים num1, num2 ו-num3 יצרנו על מנת לבדוק את מספר הריצות של הלולאה.
כעת, אם נשלח לפונקציה זו מערך בן 11 אלמנטים נוכל לקבל את התוצאה הבאה:
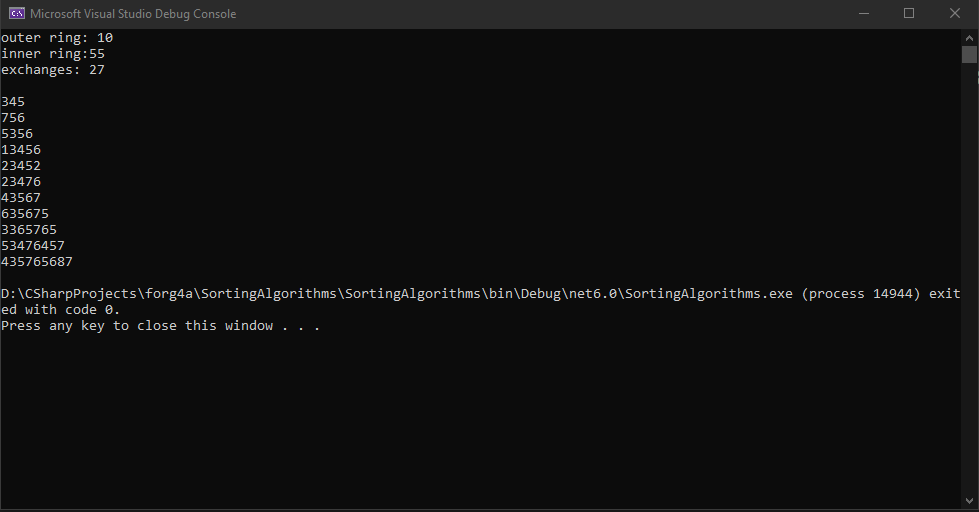
שימו לב למספר הריצות:
- נכנסו ללולאה החיצונית 10 פעמים
- נכנסנו ללולאה הפנימית 55 פעמים
- פנינו לפונקציית ההחלפה שלנו 27 פעמים
נחזור לכך בהמשך, כאשר נרצה להשוות את התוצאות של כל האלגוריתמים.
Selection Sort
ב-Selection Sort נשתמש על מנת לנסות לצמצם את הפעמים שאנו קוראים לפונקציית ההחלפה.
אופן הפעולה של אלגוריתם זה מזכיר מעט את זה של Bubble Sort,
אך מספר הריצות יהיה שונה באופיו.
נצטרך ליצור שני פונקציות לשם כך:
public static int ArrayMinInt(int[] data, int start, ref int count)
{
int min = start;
for (int position = start + 1; position < data.Length; position++)
{
count++;
if (data[position] < data[min])
{
min = position;
}
}
return min;
}
public static string IntArraySelectionSort(int[] data)
{
int num1 = 0, num2 = 0, num3 = 0, finalnum2 = 0;
for (int i = 0; i < data.Length - 1; i++)
{
num1++;
if (i != ArrayMinInt(data, i, ref num2))
{
Exchange(data, i, ArrayMinInt(data, i, ref finalnum2), ref num3);
}
}
return $"IntArraySelectionSort runs: {num1}\nIntArrayMin runs: {finalnum2}\nExchanges: {num3}";
}
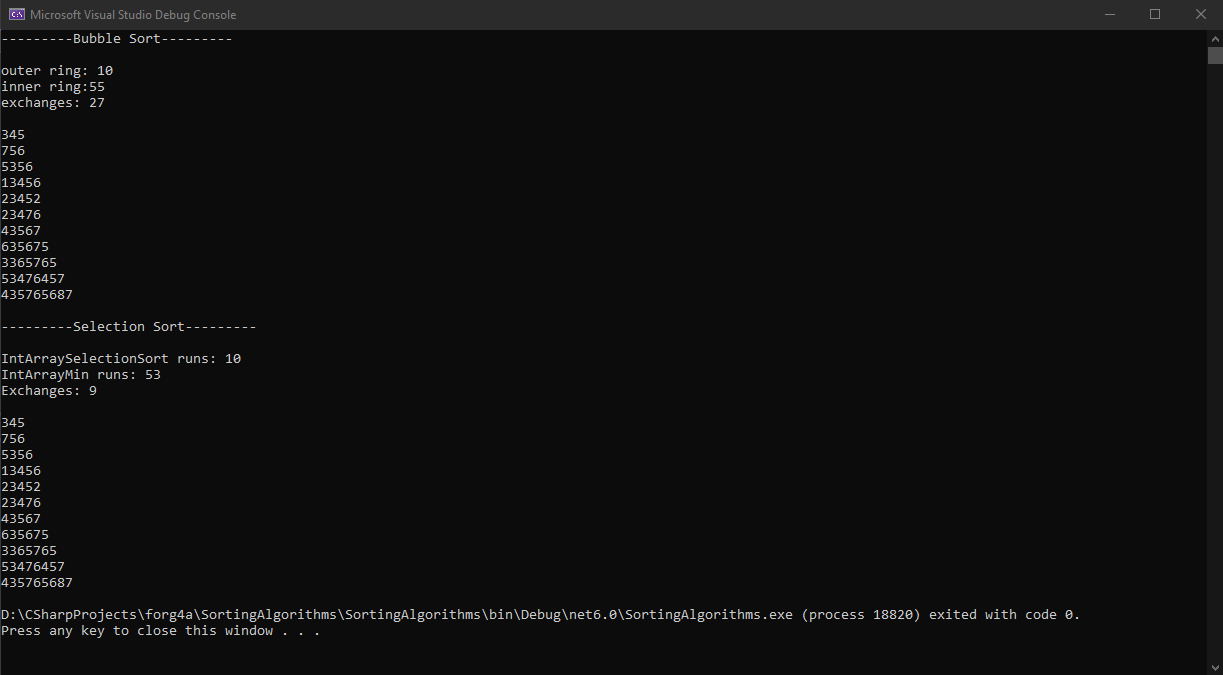
מיד תוכלו להבין שמספר הריצות בלולאה החיצונית נשאר על כנו,
הלולאה שבפונקציה – IntArrayMin (הלולאה הפנימית) רצה 53 פעמים – שיפור קטן לעומת Bubble Sort.
אך לפונקציית ההחלפה נשלחו פחות בקשות בפעם הזו (9).
כלומר ששימוש באלגוריתם זה אכן משתמש פחות פעמים בפונקציה Exchange,
מה שיכול להוביל לשיפור קל בביצועים.
Insertion Sort
עקרון הפעולה של אלגוריתם זה הוא כזה שנבנית רשימה חדשה מסודרת, החל מהאלמנט הראשון.
במקרה זה נצטרך לקרוא לפונקציה Exchange את אותו מספר הפעמים כמו ב-Bubble Sort,
אך מספר הריצות בלולאות יהיה כמספר הפעמים שנצטרך להשתמש בפונקציית ההחלפה:
public static string InsertionSort(int[] data)
{
int num1 = 0, num2 = 0, num3 = 0;
for (int j = 1; j < data.Length; j++)
{
num1++;
for (int i = j; i > 0 && data[i] < data[i - 1]; i--)
{
num2++;
Exchange(data, i, i - 1, ref num3);
}
}
return $"outer ring: {num1}\ninner ring:{num2}\nexchanges: {num3}";
}
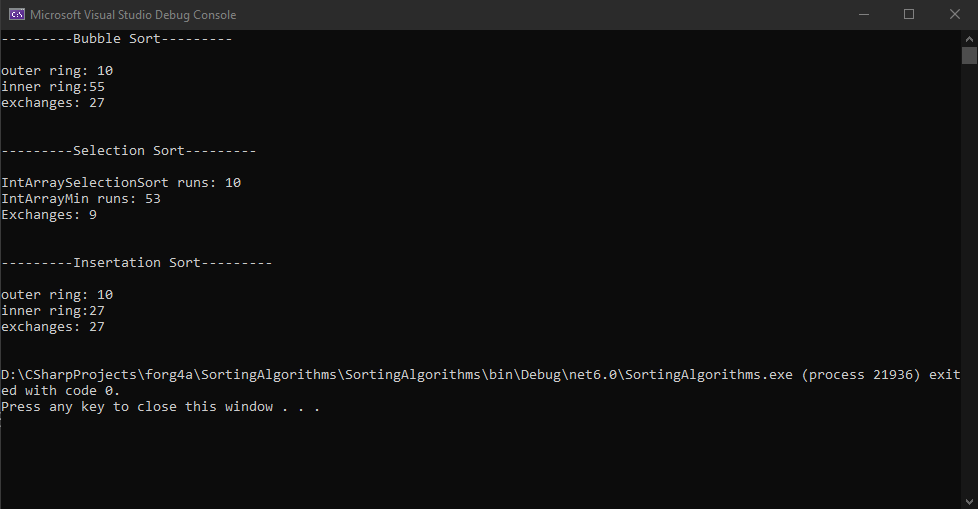
Shell Sort
ניתן לומר כי אלגוריתם זה הוא למעשה דרך יפה לשפר את Insertation Sort.
עקרון הפעולה שלו הוא כזה שלעומת Insertation שמסיר אינטרוול על כל החלפה,
ה-Shell sort מחליף חלקים שהם רחוקים אחד מהשני.
על ידי שימוש בפתרון זה, ניתן להקטין מעט את מספר הריצות הנדרש, אך מספר ההחלפות תישאר זהה:
static int[] GenerateIntervals(int num)
{
if (num < 2)
{ // no sorting will be needed
return new int[0];
}
int t = Math.Max(1, (int)Math.Log(num, 3) - 1);
int[] intervals = new int[t];
intervals[0] = 1;
for (int i = 1; i < t; i++)
{
intervals[i] = 3 * intervals[i - 1] + 1;
}
return intervals;
}
public static string ShellSort(int[] data)
{
int num1 = 0, num2 = 0, num3 = 0, num4 = 0, num5 = 0;
int[] intervals = GenerateIntervals(data.Length);
for (int k = intervals.Length - 1; k >= 0; k--)
{
num1++;
int interval = intervals[k];
for (int m = 0; m < interval; m++)
{
num2++;
for (int j = m + interval; j < data.Length; j += interval)
{
num3++;
for (int i = j; i >= interval && data[i] < data[i - interval]; i -= interval)
{
Exchange(data, i, i - interval, ref num4);
}
}
}
}
return $"Outer ring: {num1}\nMiddle ring:{num2}\nInner ring: {num3}\nExchanges: {num4}";
}
ראשית יצרנו פונקציה שתחזיר לנו את מספר האינטרוולים, ופונקציית המיון תסיר אינטרוול אחרי כל החלפה.
כך שלמעשה מספר ההחלפות יישאר זהה, אך מספר הריצות הנדרשות יופחת:
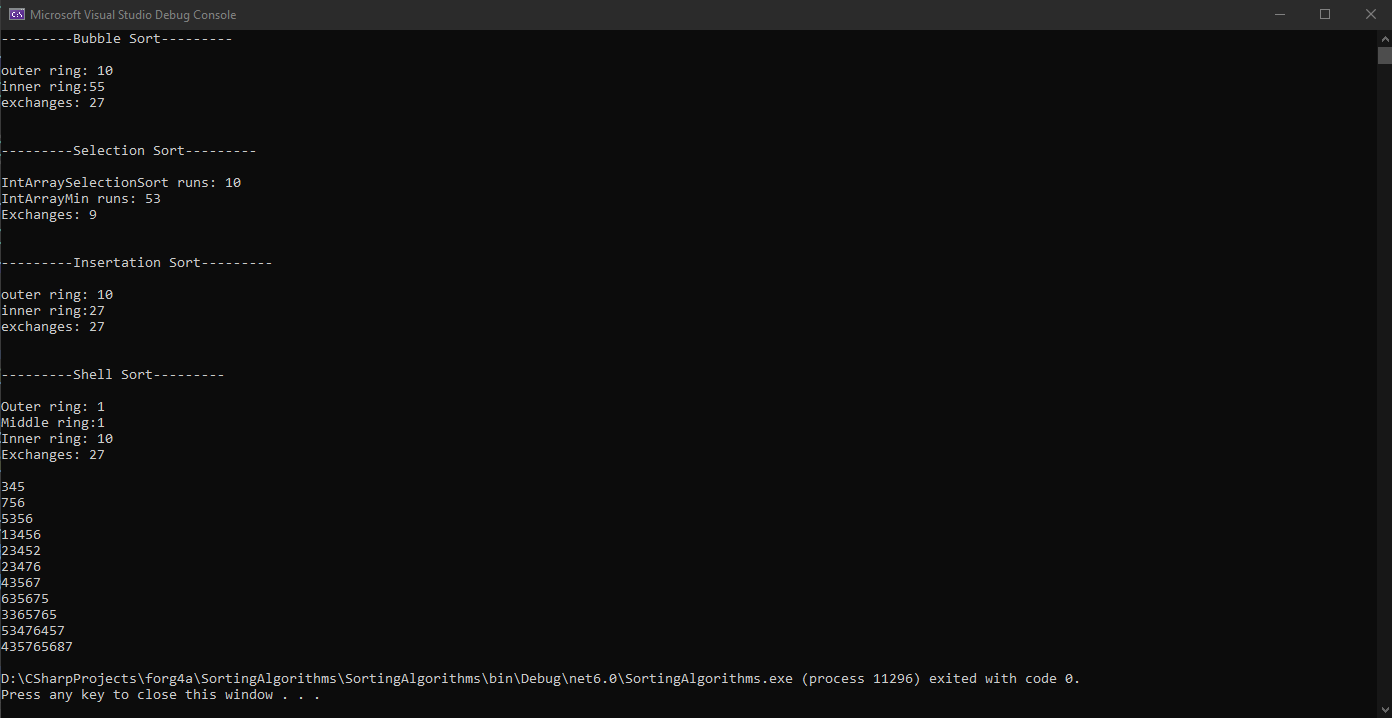
Quick Sort
אלגוריתם רקורסיבי זה, נחשב למהיר שבחבורה.
למעשה אם יש לנו רשימה מסוג List שנפעיל עליה את הפונקציה המובנית ()Sort,
מה שיקרה מאחורי הקלעים נראה בערך כך מבחינה לוגית:
public static void QuickSort(int[] data, int l, int r)
{
int i = l;
int j = r;
int x = data[(l + r) / 2];
while (true)
{
while (data[i] < x)
{
i++;
}
while (x < data[j])
{
j--;
}
if (i <= j)
{
Exchange(data, i, j);
i++;
j--;
}
if (i > j)
{
break;
}
}
if (l < j)
{
QuickSort(data, l, j);
}
if (i < r)
{
QuickSort(data, i, r);
}
}
public static void QuickSort(int[] data)
{
QuickSort(data, 0, data.Length - 1);
}
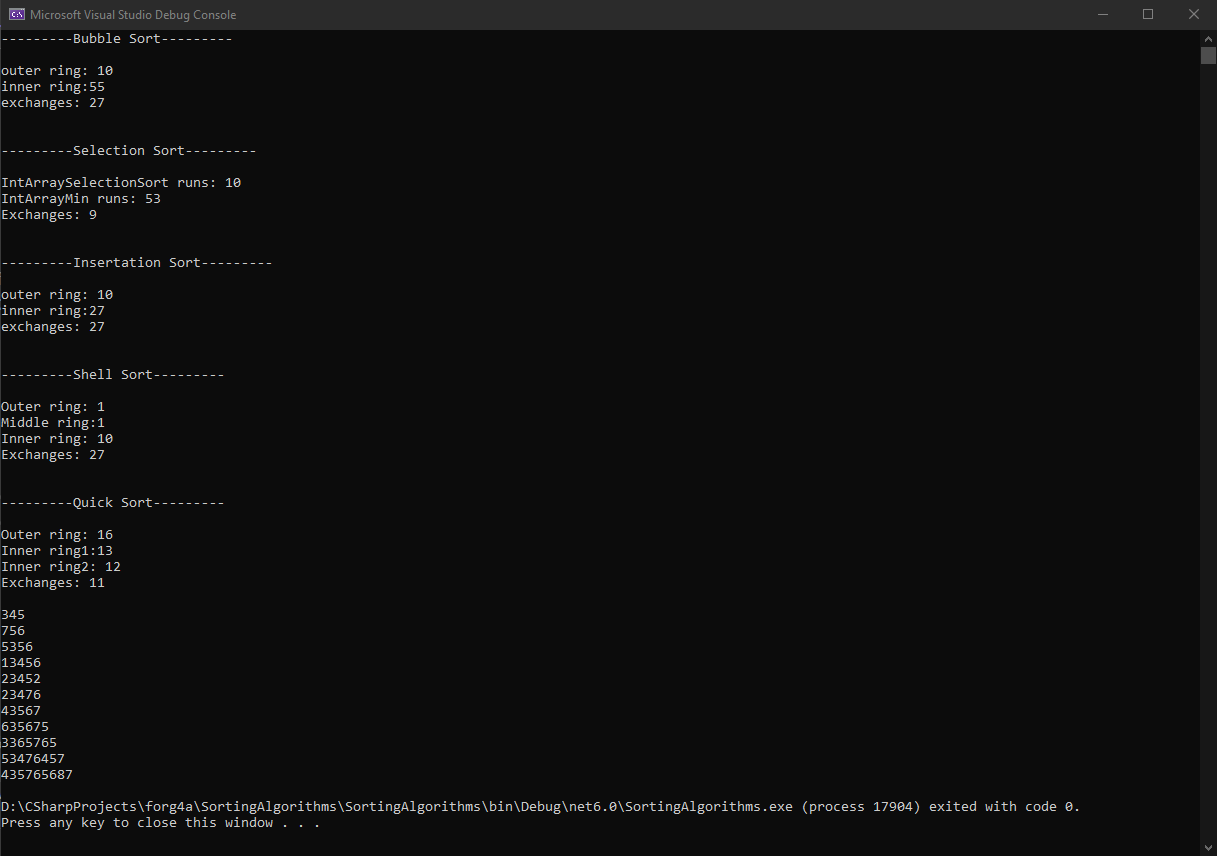
שימו לב לתוצאות שקיבלנו מ-Quick Sort, אלו הביצועים הטובים ביותר שקיבלנו עד כה מבחינת מהירות.
כמובן שאורך של מערך ואופי הנתונים יכול להשפיע על תוצאות,
כך שאין זה הכרח שזהו הפתרון הטוב עבורנו אם מה שאנחנו מחפשים זה לחסוך במשאבי זיכרון למשל.
אם נבדוק במשך כמה זמן רץ כל אלגוריתם על מערכים שונים, נקבל תוצאות כאלו:
קידוד מהנה!